NumPy常见运算
加减乘除幂
在 NumPy 中,基本的加减乘除,乘幂运算如下:
- 加法:使用 + 运算符或
numpy.add()函数 - 减法:使用 - 运算符或
numpy.subtract()函数 - 乘法:使用 * 运算符或
numpy.multiply()函数 - 除法:使用 / 运算符或
numpy.divide()函数 - 乘幂:使用 ** 运算符或
numpy.power()函数
相同形状的数组之间运算遵循对应元素相加的原则,在此不再赘述。
广播原则
NumPy 的广播原则 (broadcasting) 指定了不同形状的数组之间的算术运算规则,将形状较小的数组扩展为与形状较大的数组相同,再进行运算,以提高效率。
一维数组和标量
一维数组的每个元素分别和标量进行运算,下面是使用例:
arr1 = np.arange(-2, 2+1)
arr2 = np.array([2])
print(np.add(arr1, arr2))
# [0 1 2 3 4]
print(np.multiply(arr1, arr2))
# [-4 -2 0 2 4]
提示
二维数组和标量同样也是对应元素相加
一维数组和列向量
将广播原则用在一维数组和列向量的加法和乘法上。以 [-2, -1, 0, 1, 2] 和 [[1], [2], [3]] 相加为例,广播过程相当于把一维数组 (1, 5) 展成 (3, 5) 二维数组,把列向量 (3, 1) 也展成 (3, 5) 二维数组。然后对应元素相运算,运算结果也是二维数组。
arr1 = np.arange(-2, 2+1)
arr2 = np.array([1, 2, 3]).reshape(3, 1)
print(np.add(arr1, arr2))
# [[-1 0 1 2 3]
# [ 0 1 2 3 4]
# [ 1 2 3 4 5]]
print(np.multiply(arr1, arr2))
# [[-2 -1 0 1 2]
# [-4 -2 0 2 4]
# [-6 -3 0 3 6]]
二维数组和一维数组
二维数组和一维数组之间的广播原则运算。若二维数组的形状为 (4, 6),一维数组的形状为 (1, 6 ),则一维数组会被拓展成形状为 (4, 6) 的二维数组。
注意
注意,当前 NumPy 不支持 (4, 6) 和 (1, 4) 之间的广播运算,会报错。这种情况,要用 (4, 6) 和 (4, 1) 之间的广播原则,即二维数组与列向量的广播原则。


常见函数
NumPy 还提供大量常用函数,如下图所示。
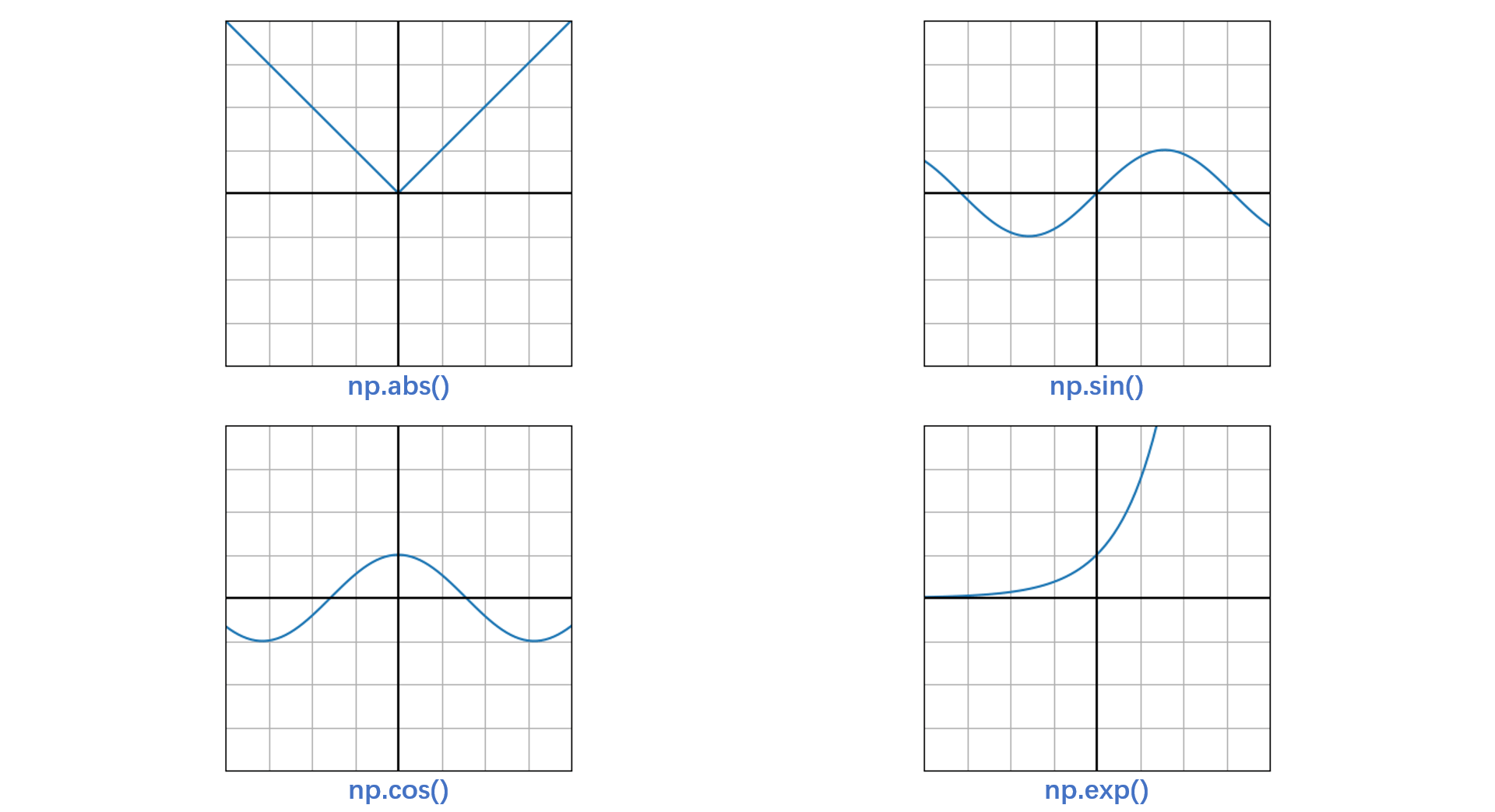
NumPy 中还给出很多常用常数,比如 numpy.pi (圆周率)、numpy.e (欧拉数、自然底数)、numpy.Inf (正无穷)、numpy.NAN (非数) 等等。
统计运算
求最大值
给定二维数组 A,A.max() 计算整个数组中最大值。而 A.max(axis=0) 取得二维数组每一列的最大值,结果为一维数组。A.max(axis=1) 取得每一行的最大值,结果同样为一维数组。而 A.max(axis=1, keepdims=True) 的结果为列向量。下面是使用例:
import numpy as np
A = np.array([[4, 3, 3, 8, 9, 9],
[0, 8, 2, 4, 1, 1],
[7, 7, 6, 7, 8, 6]])
Max = A.max()
# 9
Max_axis0 = A.max(axis=0)
# [7 8 6 8 9 9]
Max_axis1 = A.max(axis=1)
# [9 8 8]
求和
给定二维数组 A,A.sum() 对整个数组求和。而 A.sum(axis=0) 取得二维数组每一列的和,结果为一维数组。A.sum(axis=1) 取得每一行的和,结果同样为一维数组。而 A.sum(axis=1, keepdims=True) 的结果为列向量。下面是使用例:
import numpy as np
A = np.array([[4, 3, 3, 8, 9, 9],
[0, 8, 2, 4, 1, 1],
[7, 7, 6, 7, 8, 6]])
Sum = A.sum()
# 93
Sum_axis0 = A.sum(axis=0)
# [11 18 11 19 18 16]
Sum_axis1 = A.sum(axis=1)
# [36 16 41]
求平均值
给定二维数组 A,np.average(A) 对整个数组求平均值。而 np.average(A, axis=0) 取得二维数组每一列的平均值,np.average(A, axis=1) 取得每一行的平均值,结果为一维数组。下面是使用例:
import numpy as np
A = np.array([[4, 3, 3, 8, 9, 9],
[0, 8, 2, 4, 1, 1],
[7, 7, 6, 7, 8, 6]])
Average = np.average(A)
# 5.167
Average_axis0 = np.average(A, axis=0)
# 3.667 6. 3.667 6.333 6. 5.333
Average_axis1 = np.average(A, axis=1)
# 6. 2.667 6.833
其它运算
以二维矩阵 A 为例
| 描述 | 函数 |
|---|---|
| 计算整个二维数组的方差 | np.var(A) |
| 计算二维数组每一列的方差 | np.var(A, axis = 0) |
| 计算二维数组每一列的方差并将分母设为n - 1 | np.var(A, axis = 0, ddof = 1) |
| 计算二维数组每一列的标准差 | np.std(A, axis = 0) |
| 二维数组转置 | A.T |
| 计算整个二维数组的协方差矩阵 | np.cov(A.T, ddof = 1) |
| 计算整个二维数组的相关性系数矩阵 | np.corrcoef(iris_data_array.T) |
待补充待补充
numpy.percentile()、numpy.quantile()、numpy.median()、numpy.nanmean()、numpy.nanmedian(),numpy.nanstd()、numpy.nanvar()......